Ученые нашли способ идентифицировать динамику в хаотических системах

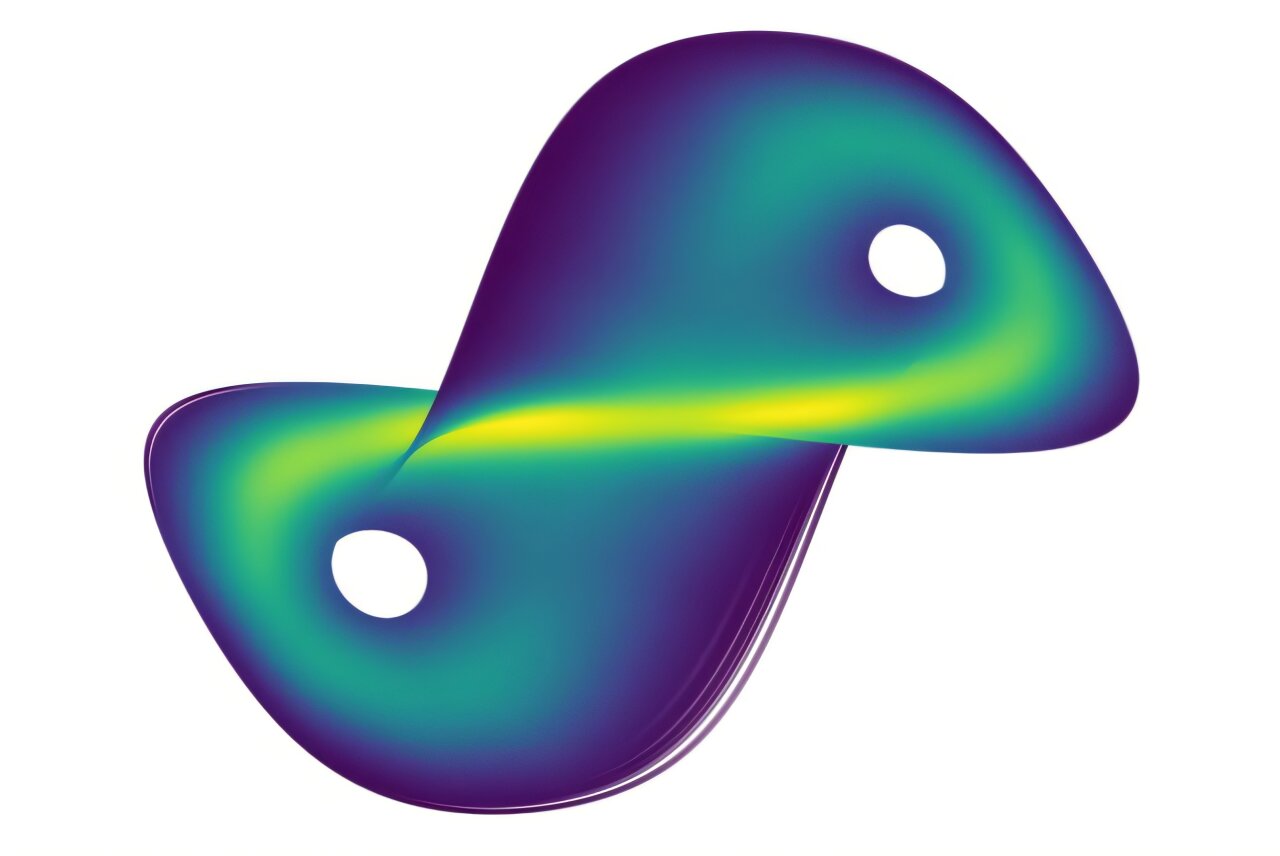
Пример инвариантной меры для упрощенной математической модели атмосферной конвекции, известной как система Лоренца-63, с использованием метода исследователей с временными задержками. Автор: Джона Ботвиник-Гринхаус

Многие важнейшие системы мира, такие как атмосфера, турбулентные жидкости и даже движение планет, ведут себя непредсказуемо из-за хаоса и шума. Ученые часто изучают эти системы через их «инвариантные» меры — долгосрочные статистические поведения, а не отдельные траектории. Хотя это полезно, у этих мер есть фундаментальное ограничение: совершенно разные системы могут иметь одинаковую статистику, что делает невозможным идентификацию лежащей в основе динамики.

Исследователи под руководством математика Юнань Ян предложили новый подход, использующий снимки с временной задержкой. Их работа «Инвариантные меры в координатах с временной задержкой для уникальной идентификации динамических систем» была опубликована в журнале Physical Review Letters 17 октября.

Инвариантная мера — это способ присвоения размера или вероятности частям системы, которые остаются неизменными при преобразовании или эволюции системы. Снимки с временной задержкой используют инвариантные меры, выраженные в координатах с временной задержкой — связывая текущие наблюдения с их прошлыми значениями — и предоставляют достаточно информации для различения систем.

Преобразуя эти теоретические результаты в вычислительные инструменты, исследователи смогли продемонстрировать их эффективность на физических примерах.

«Этот прорыв предлагает надежный метод для раскрытия правил, лежащих в основе сложных явлений, открывая новые возможности для таких задач, как прогнозирование погоды, проектирование космических аппаратов и анализ хаотических данных в науке и технике», — сказала Ян, ассистент-профессор математики в Колледже искусств и наук.

Соавторами статьи стали Джона Ботвиник-Гринхаус, докторант в области прикладной математики, и Роберт Мартин из Армейской исследовательской лаборатории DEVCOM.

Ян сказала, что ее привлекла эта тема, потому что она похожа на решение головоломки.

«Вам даны данные, которые представляют некоторую лежащую в основе физику или инженерные величины, и ваша задача — действительно распутать данные и увидеть, что их вызывает. Но проблема в том, что когда вы не можете однозначно идентифицировать величины — есть две разные модели, которые дают вам одинаковые данные, поэтому вы не можете их различить. Нам нужно иметь уникальное представление, такова мотивация нашей работы».

Их метод может быть применен для ответа на вопросы в биологии, поскольку живые существа меняются со временем; в психологии, поскольку люди меняют свое поведение со временем; в технике, например, сопротивление воздушного потока на самолетах или поток трафика, и в других областях.

«Мы используем уравнения временной динамики для моделирования основных причин, и это может быть так же важно, как вероятность передачи вирусов, таких как COVID», — сказала Ян.

Работа заняла более года, но Ян говорит, что никогда не боялась застрять.

«Математики всегда имеют дело с проблемами, не имеющими ответа. Нам нравятся вызовы».

Больше информации: Jonah Botvinick-Greenhouse et al. Invariant Measures in Time-Delay Coordinates for Unique Dynamical System Identification, Physical Review Letters (2025). DOI: 10.1103/ppys-lx68, journals.aps.org/prl/abstract/10.1103/ppys-lx68

Источник: Cornell University

Исследование хаотических систем имеет важное практическое значение. Например, система Лоренца-63, упомянутая в работе, была одной из первых математических моделей, демонстрирующих хаотическое поведение, и заложила основы современной теории хаоса в 1960-х годах. Новый метод может найти применение в улучшении прогнозов погоды, где небольшие начальные погрешности могут привести к совершенно разным результатам — явление, известное как «эффект бабочки».