Разработан устойчивый метод усреднения данных на искривленных пространствах

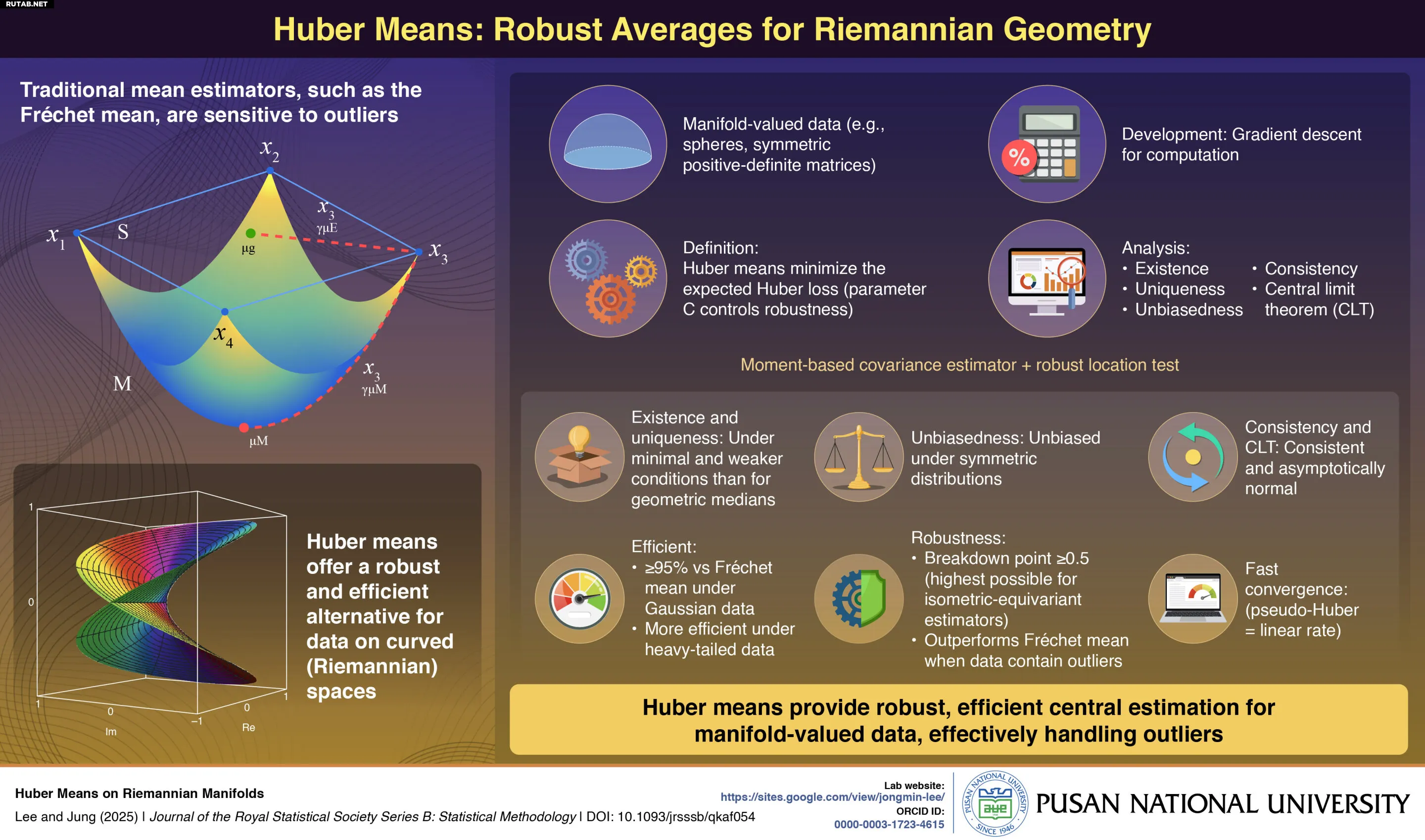
Ученые разработали новый статистический метод под названием «среднее Хубера», который обеспечивает более стабильный и надежный способ вычисления средних значений для данных, расположенных на искривленных геометрических пространствах, известных как многообразия Римана. Сочетая преимущества методов наименьших квадратов (L₂) и наименьших абсолютных отклонений (L₁), среднее Хубера устойчиво к искажениям от выбросов, сохраняя при этом эффективность. Это улучшает анализ данных в таких областях, как медицинская визуализация, робототехника и искусственный интеллект.

В эпоху, управляемую сложными данными, ученые все чаще сталкиваются с информацией, которая не лежит на плоских евклидовых поверхностях. От 3D-медицинских сканов до ориентаций роботов и преобразований в ИИ — многие современные данные существуют на искривленных геометрических пространствах. Точный анализ таких данных остается сложной задачей, особенно когда шум или выбросы искажают результаты.

Чтобы решить эту проблему, профессор Чонмин Ли из Национального университета Пусана в сотрудничестве с профессором Сунгкю Чжоном из Сеульского национального университета разработал новый статистический метод, названный средним Хубера, предназначенный для повышения устойчивости и надежности анализа данных на искривленных пространствах. Исследование, опубликованное в «Journal of the Royal Statistical Society Series B: Statistical Methodology» 25 августа 2025 года, представляет собой устойчивое обобщение классического среднего Фреше путем интеграции функции потерь Хубера, объединяя эффективность и устойчивость к выбросам в одной элегантной структуре.

«Наше исследование представляет собой устойчивое обобщение классического среднего Фреше на многообразиях Римана, — сказал Ли. — Это обеспечивает большую стабильность против выбросов и повышает надежность статистического анализа геометрических данных».

Среднее Хубера автоматически адаптируется к структуре данных, используя потери L₂ (наименьшие квадраты) для типичных наблюдений и потери L₁ (абсолютные отклонения) для больших отклонений. Этот баланс позволяет ему достичь точки breakdown в 0,5, что означает, что оценка остается надежной, даже если половина данных являются выбросами или экстремальными значениями. Исследование также предоставляет теоретические гарантии существования, уникальности, сходимости и несмещенности оценщика, а также новый вычислительный алгоритм, который быстро сходится на практике.

«Этот метод позволяет проводить более устойчивый анализ данных в неевклидовых настройках, что имеет потенциальные применения в таких областях, как компьютерное зрение, медицинская визуализация и анализ форм», — пояснил Ли.

Эти применения распространяются на научные и инженерные области. В медицинской визуализации среднее Хубера может улучшить усреднение данных о форме мозга или органов, что приведет к более точным диагнозам. В робототехнике оно может помочь системам лучше интерпретировать данные о движении и ориентации, даже в зашумленных или непредсказуемых средах. В ИИ и машинном обучении оно может сделать модели, работающие с геометрическими данными (связанные вращения, графы или преобразования), более устойчивыми и справедливыми.

«Предоставляя основу для устойчивого и геометрически осознанного анализа данных, это исследование может незаметно лечь в основу следующего поколения надежного ИИ, прецизионной медицины и интеллектуальных технологий, которые взаимодействуют с реальным миром», — добавил Ли.

Дополнительная информация: Jongmin Lee et al, Huber means on Riemannian manifolds, Journal of the Royal Statistical Society Series B: Statistical Methodology (2025). DOI: 10.1093/jrsssb/qkaf054