Новый подход на основе тензорных сетей улучшит моделирование квантовых систем

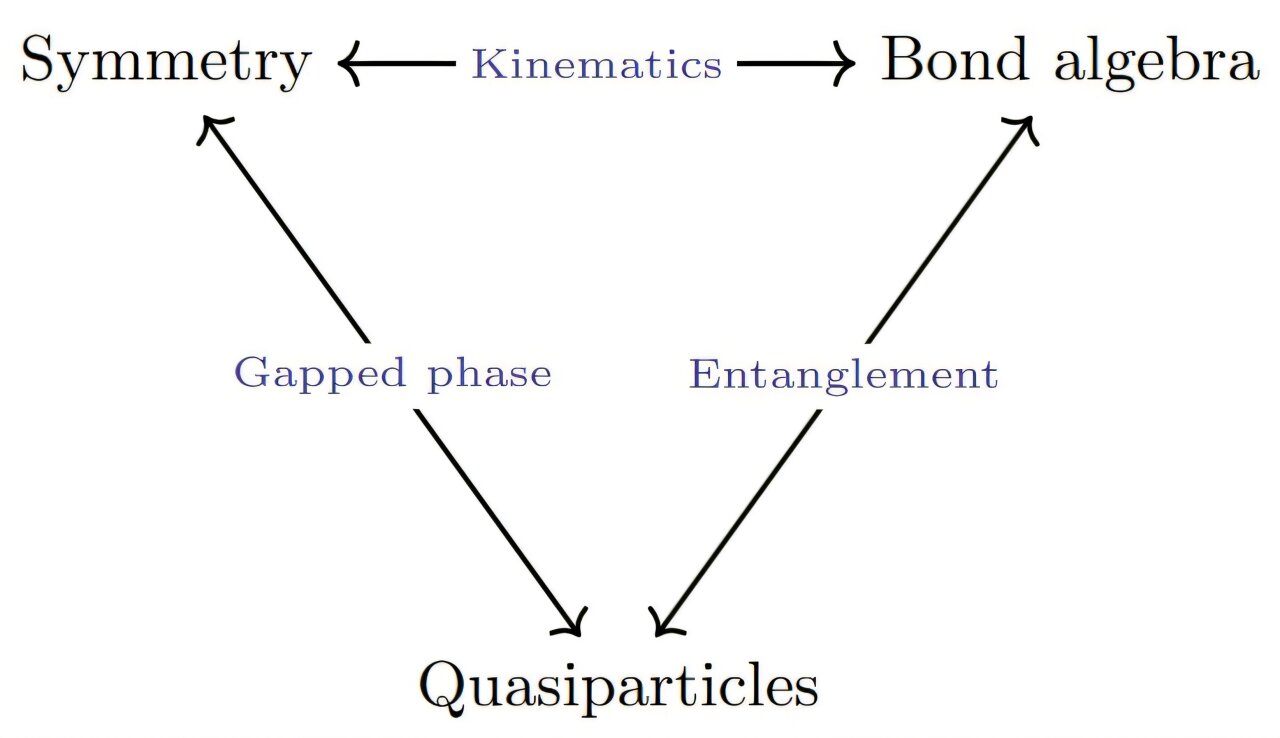
Схематическая диаграмма, иллюстрирующая связи между категориальными структурами, описывающими различные свойства низкоэнергетических состояний квантовой спиновой цепи. Автор: Лутенс, Делькамп и Верстрате.

Исследователи из Кембриджского университета, Института высших научных исследований и Гентского университета представили новую стратегию на основе тензорных сетей, которая может продвинуть моделирование квантовых многочастичных систем. Их подход, описанный в статье, опубликованной в журнале Nature Physics, позволяет эффективно моделировать квантовые решёточные модели, которые сложно симулировать традиционными методами.

Как объяснил ведущий автор работы Лоренс Лутенс, недавние исследования укрепили позиции матричных продукт-операторов как правильного языка для изучения обобщённых глобальных симметрий одномерных квантовых систем. Математически такие симметрии кодируются в структурах, обобщающих обычные группы, называемых категориями слияния.

«В нашей недавней работе мы стремились объединить теоретический компонент, касающийся теории представлений обобщённых симметрий, с хорошо зарекомендовавшими себя вариационными методами оптимизации матричных продукт-состояний», — пояснил Лутенс.

Используя теорию представлений матричных продукт-операторов для обобщённых симметрий, исследователи доказали, что любую одномерную квантовую гамильтонову систему с симметрией можно отобразить на эквивалентную двойственную гамильтонову систему с точно таким же спектром, но основное состояние которой спонтанно нарушает полную двойственную симметрию.

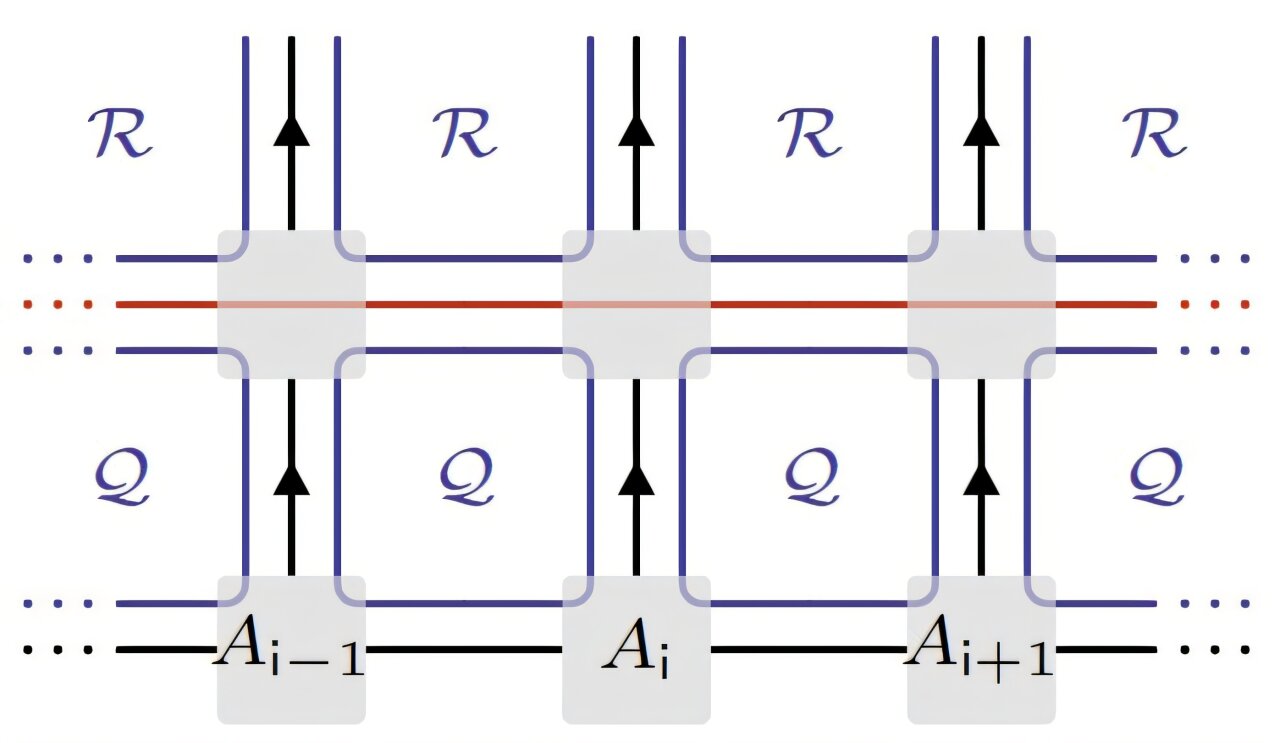
Действуя матричным продукт-оператором, можно получить общее основное состояние из симметрийно-нарушенного с меньшим количеством вариационных параметров. Автор: Лутенс, Делькамп и Верстрате.

Этот подход позволяет получать симметрийно-нарушенные основные состояния квантовых многочастичных систем гораздо эффективнее, чем симметрийные методы, поскольку последние обычно накладывают избыточность в паттернах запутанности, вычисление которых требует больших затрат.

«Отображение на модель с нарушением симметрии устраняет эту избыточность и раскрывает математическую структуру, лежащую в основе основного состояния, а также его спектра квазичастичных возбуждений», — сказал Лутенс.

Метод, разработанный исследователями, находится на стыке математических и вычислительных стратегий и может превзойти традиционные подходы на основе тензорных сетей в эффективном представлении квантовых многочастичных систем и их основных состояний.

В текущем исследовании команда применила свой метод к изучению одномерных квантовых систем. В будущем они надеются распространить его на более сложные многочастичные системы высших размерностей.