Математическое доказательство проливает свет на процессы смешивания
Слои математических формул белым текстом на тёмном фоне. Автор: Эрика Фукухара/OIST, с использованием уравнений из работы Ishige et al., Math. Ann., 2025.
Что происходит, когда вещи смешиваются? Этот вопрос лежит в основе неравенства Борелла-Браскампа-Либа (BBL) — математического соотношения, широко применяемого в различных областях математики, науки и не только.
Исследователи из Окинавского института науки и технологий (OIST), Токийского университета и Университета Флоренции представили новое доказательство этого мощного неравенства, используя нестандартный подход на основе уравнений теплопроводности и диффузии. Работа опубликована в журнале Mathematische Annalen.
Математическое описание взаимодействий
«Математики давно используют неравенства для описания взаимосвязей», — объясняет профессор Цин Лю, руководитель подразделения геометрических дифференциальных уравнений в OIST и соавтор исследования.
«Неравенство Борелла-Браскампа-Либа особенно полезно для описания процессов смешивания, например, как изменяется форма или плотность при соединении двух веществ. Хотя мы знаем, что неравенства могут описывать диффузию растворов, мы хотели исследовать обратную ситуацию: можно ли, используя уравнения диффузии, глубже понять математические неравенства?»
Лю и его коллеги — профессор Казухиро Ишиге из Токийского университета и профессор Паоло Салани из Университета Флоренции — использовали нелинейные дифференциальные уравнения в частных производных (УЧП) в качестве основы для своего доказательства. УЧП описывают изменения в пространстве и времени, а в данном случае они связаны с диффузией веществ через пористые материалы.
Команда изучала геометрию таких уравнений почти 10 лет. В этом проекте они хотели расширить применение УЧП и использовать их методы для решения ключевых задач в разных областях математики.
Значение неравенства Борелла-Браскампа-Либа
Многие математические концепции имеют широкое применение и долгую историю, и BBL — одна из них. Это обобщение более известного неравенства Брунна-Минковского, которое описывает, как изменяются объёмы фигур при их объединении, и его функционального аналога — неравенства Прёкопа-Лейндлера.
Неравенство Брунна-Минковского ранее сравнивали с «осьминогом, чьи щупальца простираются далеко и широко, а форма и цвет меняются при перемещении из одной области в другую» — из-за его широкого применения.
«Представьте компьютерную графику или медицинскую визуализацию. Допустим, вы хотите создать анимацию, где одна фигура плавно превращается в другую — например, круг в квадрат», — отмечает профессор Лю. «Чтобы переход выглядел естественно, промежуточные формы должны изменяться плавно, без искажений. Используя этот принцип, специалисты могут создавать реалистичные трансформации. Это особенно полезно в медицинской визуализации, когда врачи отслеживают изменение формы органов с течением времени».
BBL расширяет идеи неравенства Брунна-Минковского, описывая, как комбинируются различные «веса» или «интенсивности», а не только формы. Это позволяет применять его к ещё более широкому кругу задач: от распределения ресурсов в экономике до обработки данных в информатике, энтропии и сжатия информации, а также моделирования неопределённостей в статистике. Вместе эти неравенства являются основой выпуклой геометрии и функционального анализа.
Однако для уверенного использования BBL и подобных неравенств в различных сценариях критически важны математические доказательства, подтверждающие их справедливость в определённых условиях.
Традиционно BBL доказывали с помощью выпуклого анализа или теории оптимального транспорта, но подход с нелинейными УЧП, использованный в этом исследовании, открыл новые перспективы понимания BBL. Подобные методы могут выявить ранее недоступные свойства, делая структуру неравенств более прозрачной и универсальной.
Расширение возможностей УЧП
Исследователи называют эту работу первым шагом в новом направлении, цель которого — изучить применение различных УЧП и доказать неравенства с их помощью. Пока работа сосредоточена на евклидовом пространстве, где определены направления и расстояния, но в будущем команда планирует исследовать другие математические ландшафты, например, метрические пространства, где направленная структура в целом отсутствует.
«Для решения давних проблем важно применять творческие подходы», — говорит профессор Лю. «В этой работе мы использовали концепции из одной области математики, чтобы получить представление о другой, и надеемся, что она послужит основой для будущих междисциплинарных исследований в математике и смежных областях».
Дополнительная информация: Kazuhiro Ishige et al, A parabolic PDE-based approach to Borell–Brascamp–Lieb inequality, Mathematische Annalen (2025). DOI: 10.1007/s00208-025-03206-6
Источник: Okinawa Institute of Science and Technology
Интересный факт: Неравенство Брунна-Минковского, на котором основано BBL, было сформулировано ещё в XIX веке и до сих пор остаётся одним из ключевых инструментов в геометрии и анализе. Его применяют даже в квантовой физике для изучения свойств сложных систем.

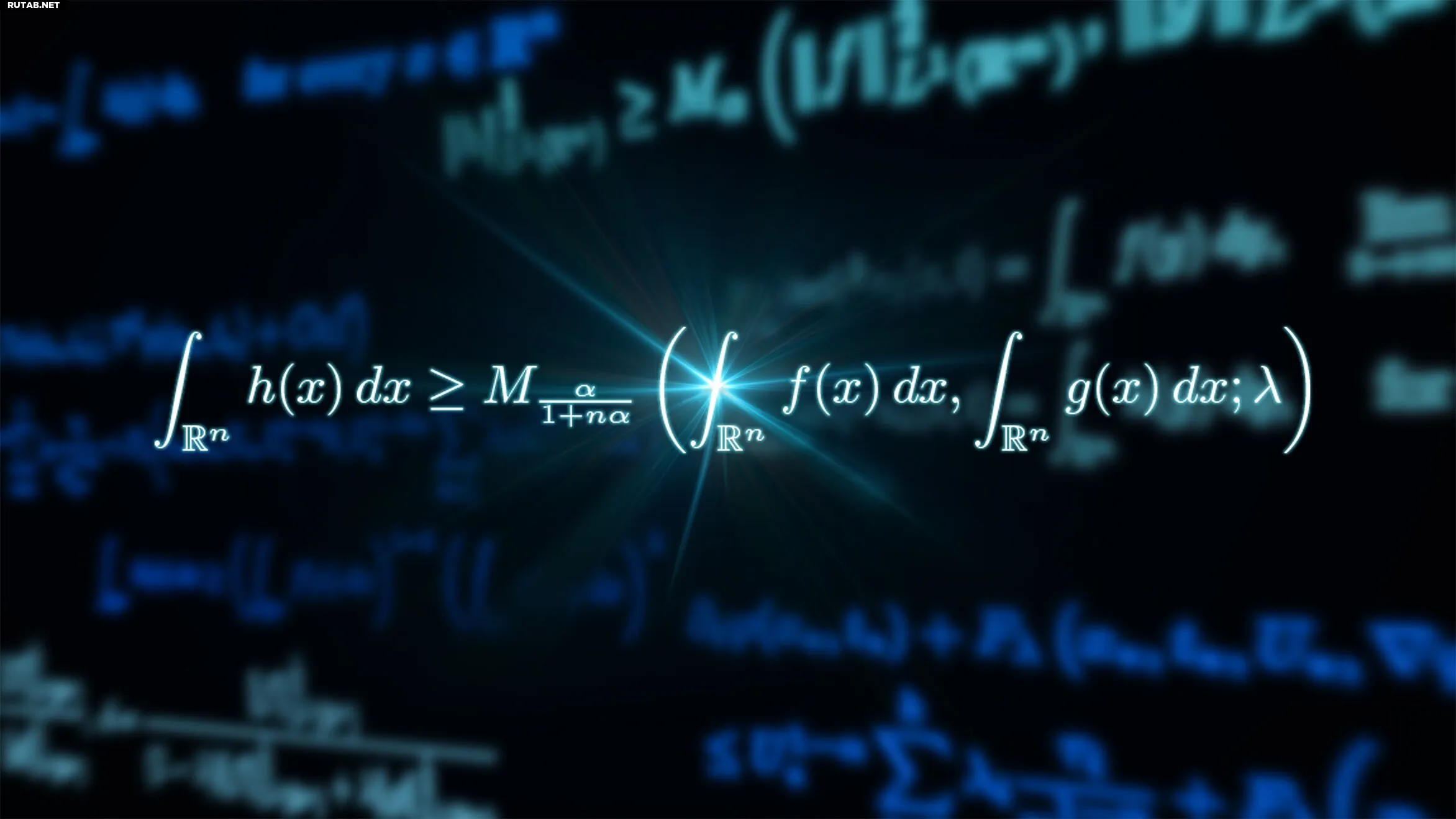






0 комментариев