Математик Теренс Тао использовал GPT-5 для решения сложной математической задачи

Искусственный интеллект снова помог известному математику Теренсу Тао решить сложную задачу!

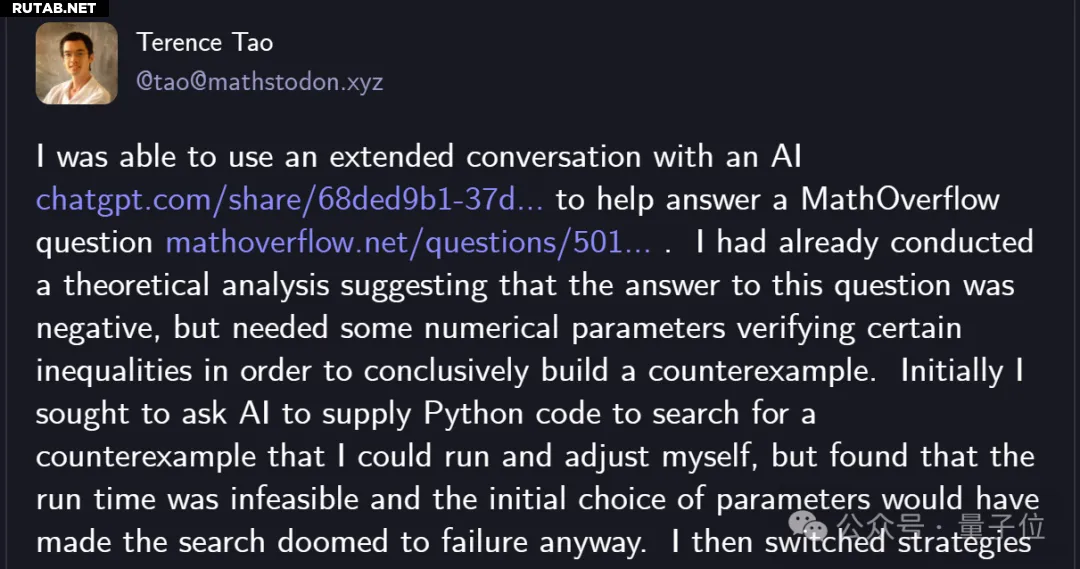
Сообщение поступило от самого Тао, который прямо заявил:

«Без помощи ИИ выполнение той же задачи заняло бы несколько часов (в основном ручное написание кода и отладка)».

Более того, без ИИ он даже не решился бы применить ту стратегию, которая в итоге привела к успеху.

«Фактически, без помощи ИИ я бы почти наверняка не стал пытаться провести такой численный поиск (возможно, попробовал бы теоретический асимптотический анализ)».

Поскольку использовался GPT-5, исследователь OpenAI Себастьен Бубек (бывший вице-президент Microsoft по ИИ и выдающийся ученый) быстро поделился этим в соцсетях, что вызвало оживленное обсуждение в сообществе.

Помимо воспоминаний о похожем опыте, пользователи сети единогласно отмечали:

«Это знаменует собой начало новой эры совместных исследований человека и машины».

Так какую же задачу решил Теренс Тао с помощью ИИ? И какую роль сыграл ИИ в этом процессе?

Давайте разберемся подробнее.

Проверка результата с помощью всего 29 строк кода на Python

Теренс Тао решал вопрос, поднятый на MathOverflow (профессиональное сообщество вопросов и ответов по математике):

Является ли последовательность lcm(1,2,…,n) подмножеством высокоизбыточных чисел?

Проще говоря, задача заключалась в сравнении двух специальных числовых последовательностей.

Одна — последовательность наименьшего общего кратного (НОК), например:

• n=2, lcm(1,2) = 2
• n=3, lcm(1,2,3) = 6
• n=4, lcm(1,2,3,4) = 12
• n=5, lcm(1,2,3,4,5) = 60
• …

Другая — последовательность высокоизбыточных чисел (Highly Abundant Numbers, HA). Эти числа обладают особым свойством: «сумма их делителей» больше, чем у любого меньшего числа.

Например, сумма делителей числа 1 равна 1, числа 2 — 3 (больше 1), числа 4 — 7 (больше 3 и 1), поэтому они являются высокоизбыточными.

Поскольку вычисленные ранее наименьшие общие кратные, как оказалось, также являются высокоизбыточными числами, возник вопрос: Всегда ли все наименьшие общие кратные будут находиться в ряду высокоизбыточных чисел? (То есть являются ли они подмножеством)

Теренс Тао ранее уже пришел к выводу через теоретический анализ, что ответ отрицательный.

Однако для полного доказательства этого факта требовалось найти конкретные числовые параметры, чтобы построить контрпример.

Хотя направление было ясным, Тао понимал, что из-за необходимости утомительных вычислений и поиска параметров это была «масштабная работа», которая вручную заняла бы несколько часов.

С GPT-5 все стало гораздо проще... Всего за несколько раундов диалога на естественном языке ИИ помог решить проблему.

Процесс выглядел следующим образом:

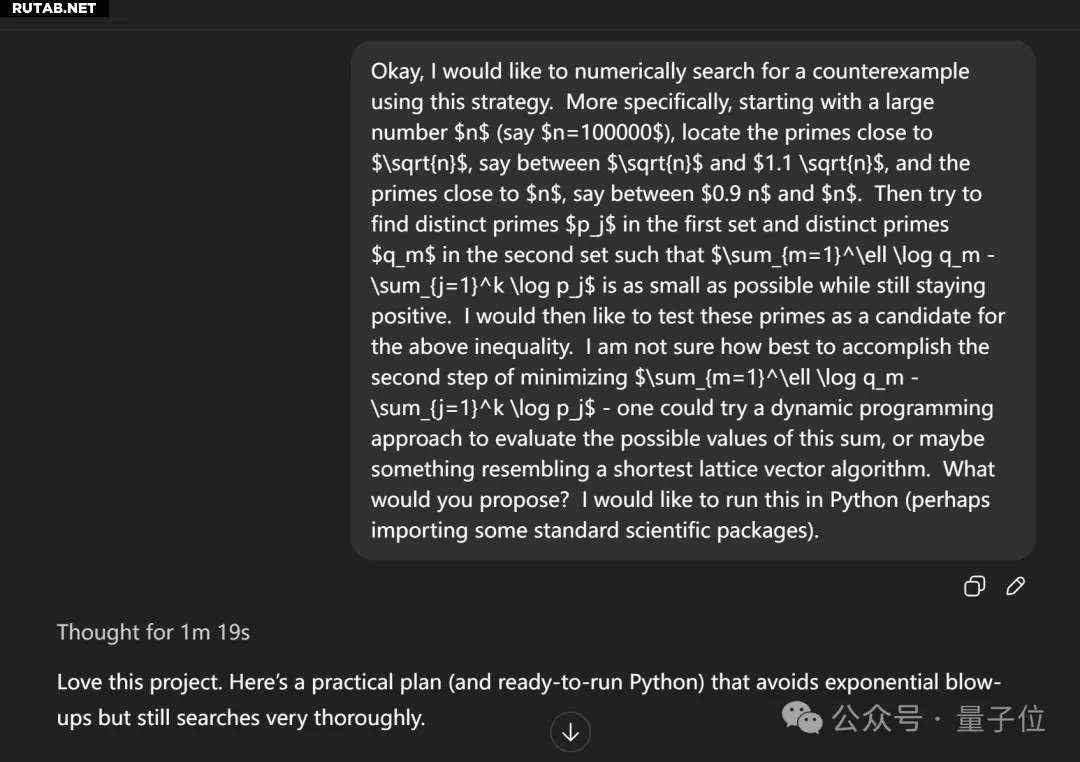
Изначально Теренс Тао попытался заставить GPT-5 сгенерировать программу на Python для поиска параметров контрпримера.

Это позволило бы ему самому запускать код и настраивать параметры.

GPT-5, подумав около 1 минуты 19 секунд, действительно выдал довольно длинный код.

Однако при запуске выяснилось, что сгенерированный код работает слишком долго, а начальные параметры выбраны неудачно, что в итоге привело к неудаче в поиске.

Тогда он изменил стратегию, начав пошаговый диалог с GPT-5, чтобы тот с помощью эвристических вычислений нашел подходящие параметры.

Другими словами, он разбил большую проблему на несколько мелких и под своим руководством поручил GPT-5 решать их по очереди.

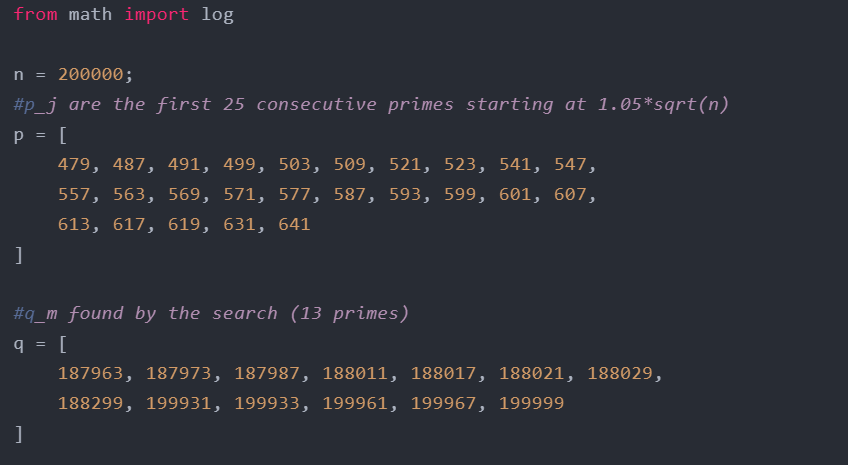
После нескольких раундов общения GPT-5 наконец успешно сгенерировал параметры, удовлетворяющие требованиям.

Более того, для обеспечения надежности результата Тао использовал сгенерированный GPT-5 Python-скрипт из 29 строк для независимой проверки.

По мнению Тао, «этот скрипт лаконичен и понятен, легко проверяется вручную, а проверенные численные результаты полностью совпадают с предыдущими эвристическими прогнозами».

Он также особо отметил, что при работе с такой серьезной областью, как математика, ИИ на этот раз не страдал от своей старой «болезни» — галлюцинаций.

«Я не столкнулся с проблемами галлюцинаций или другого бреда, порожденного ИИ».

Это не первый раз, когда Теренс Тао использует ИИ для решения математических задач

На самом деле, как ведущий математик, это не первая подобная ситуация.

Только в этом году было несколько случаев:

• В начале сентября он использовал GPT-5 для полуавтоматического поиска литературы, что позволило впервые получить proof-of-concept для проекта, связывающего проблему Эрдёша и OEIS;
• В конце мая Теренс Тао в своем блоге на YouTube наглядно продемонстрировал, как использовать только GitHub Copilot для доказательства задачи о пределе функции;
• В середине мая на своем дебютном стриме на YouTube он с помощью ИИ за 33 минуты «вслепую» доказал, что уравнение Magma E1689 влечет E2;
• В середине марта o3-mini сразу заметила и исправила его ошибку, а затем помогла быстро решить математическую задачу;
• …

По мнению Теренса Тао, «ИИ, возможно, в краткосрочной перспективе не получит Филдсовскую премию (Нобелевскую премию по математике), но он может выступать в роли посредника для математиков при проведении доказательств».

Конечно, выходя за рамки математики, пример Теренса Тао несомненно показывает нам: то, как использовать ИИ, чрезвычайно важно.

И еще кое-что

Последнее заявление генерального директора OpenAI Сэма Альтмана о GPT-5 вызывает активные обсуждения.

GPT-5 неправильно поняли!

В отличие от своей обычной уверенной позиции, на этот раз он прямо заявил, что GPT-5 представляет собой итеративное улучшение, а не внезапную смену парадигмы.

Другими словами, ожидания людей от GPT-5 были завышены (тем самым он также ответил на сбои в демонстрациях GPT-5 и жалобы на то, что возможности модели не оправдали ожиданий).

Более того, в ответ на вопрос «Когда будет достигнут ИИ?» его позиция также резко изменилась.

В отличие от прежних заявлений о том, что ИИ будет реализован до 2030 года, на этот раз он стал более осторожным, начав подчеркивать, что его больше волнуют безопасность и постепенный прогресс.

Ну что ж, парень явно мастер импровизации.

Ссылки:

[1]https://mathstodon.xyz/@tao/115306424727150237

[2]https://x.com/SebastienBubeck/status/1973977315572154383

[3]https://mathoverflow.net/questions/501066/is-the-least-common-multiple-sequence-textlcm1-2-dots-n-a-subset-of-t/501125