Учёные открыли универсальные законы квантовой запутанности во всех измерениях

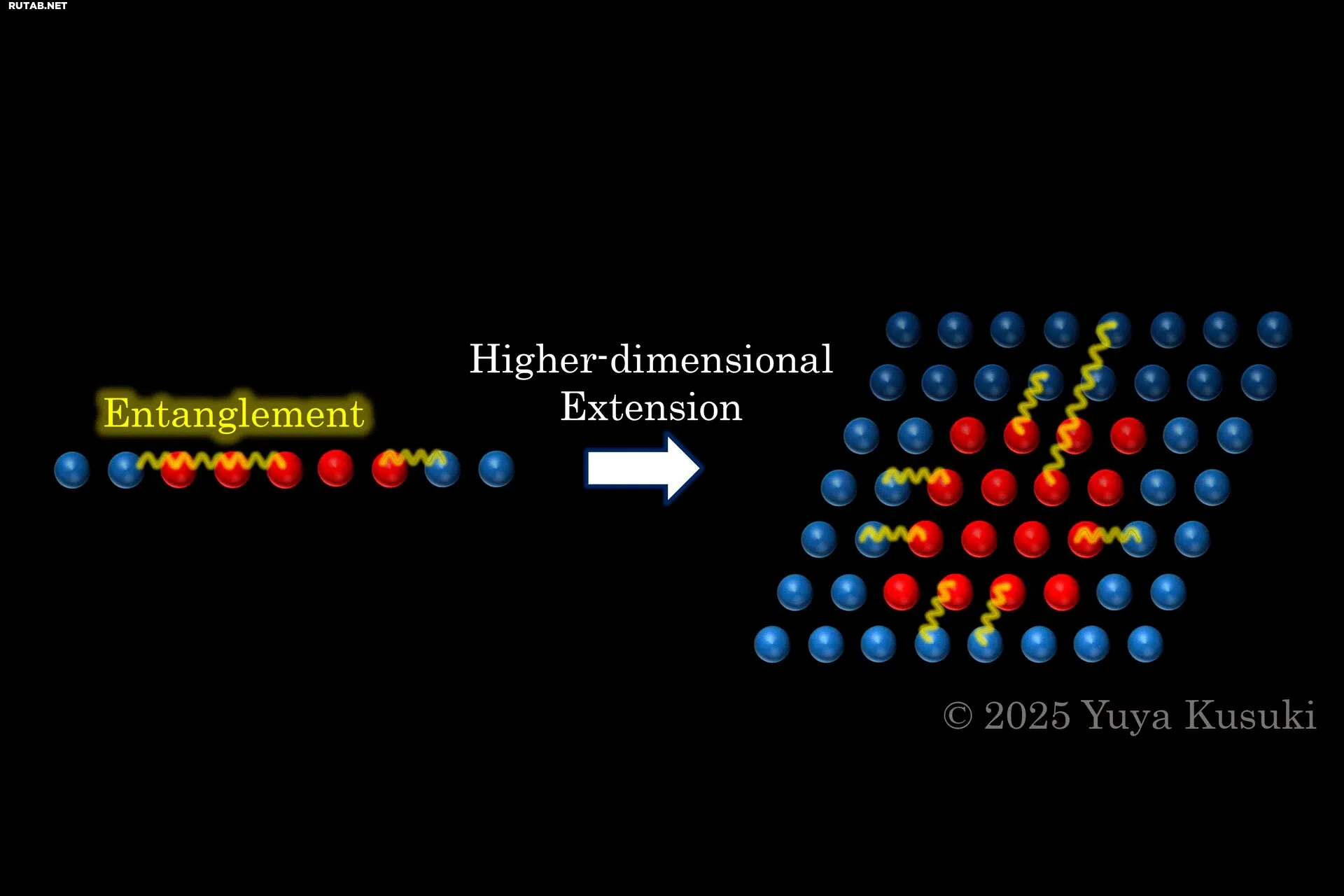
Квантовая запутанность в 1+1 и 2+1 измерениях. Автор: Юя Кусуки

Группа теоретических исследователей использовала термическую эффективную теорию, чтобы доказать, что квантовая запутанность подчиняется универсальным законам во всех измерениях. Их исследование было опубликовано в журнале Physical Review Letters.

«Это исследование — первый пример применения термической эффективной теории к квантовой информации. Результаты демонстрируют полезность этого подхода, и мы надеемся развить его дальше для более глубокого понимания структур квантовой запутанности», — заявил ведущий автор работы, доцент Института перспективных исследований Университета Кюсю Юя Кусуки.

В классической физике две частицы, находящиеся далеко друг от друга, ведут себя независимо. Однако в квантовой физике две частицы могут демонстрировать сильную корреляцию независимо от расстояния между ними. Это явление называется квантовой запутанностью.

Квантовая запутанность лежит в основе таких технологий, как квантовые вычисления и квантовая коммуникация, поэтому понимание её структуры важно как теоретически, так и практически.

Одной из ключевых мер для количественной оценки квантовой запутанности является энтропия Реньи. Она измеряет сложность квантовых состояний и распределение информации, играя важную роль в классификации квантовых состояний и оценке возможности моделирования квантовых многочастичных систем.

Кроме того, энтропия Реньи используется в теоретических исследованиях проблемы потери информации в чёрных дырах и часто встречается в контексте квантовой гравитации.

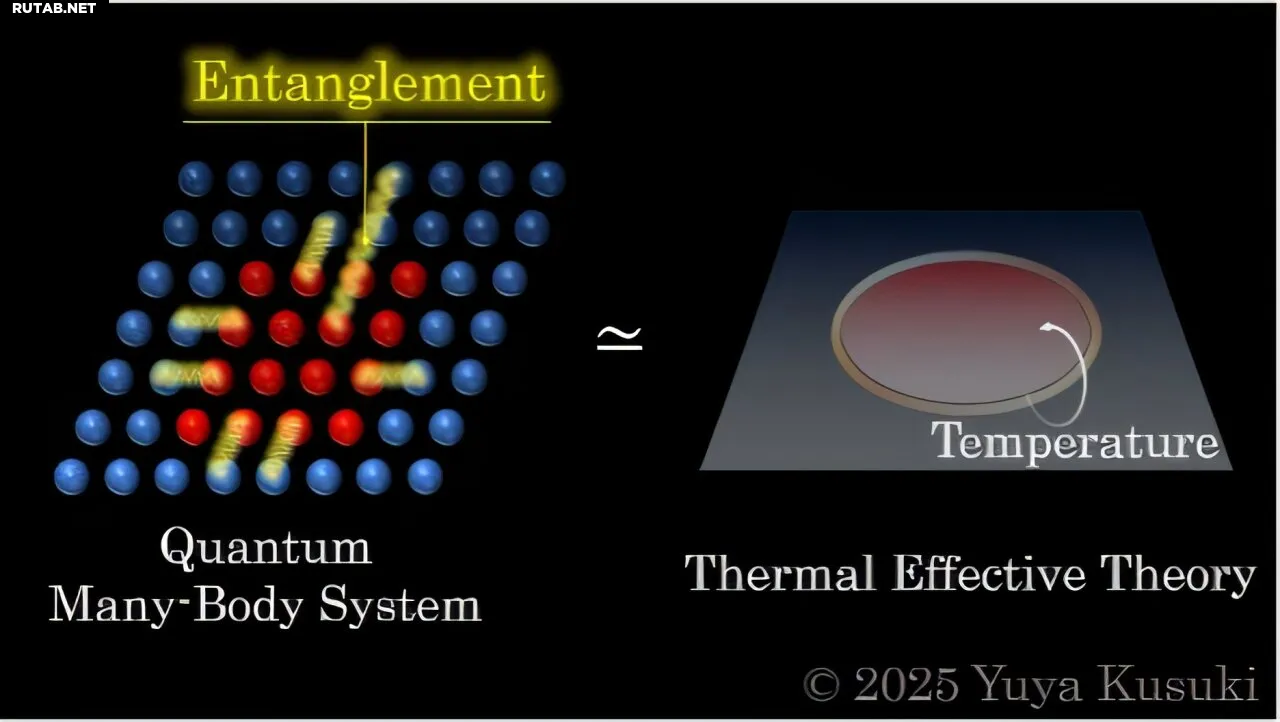
Изучение квантовой запутанности в многочастичной системе с помощью термической эффективной теории, выявляющей универсальные свойства квантовой запутанности. Автор: Юя Кусуки

Исследовательская группа под руководством Кусуки, профессора Хироси Оогури из Института физики и математики Вселенной Кавли (Токийский университет) и исследователя Калифорнийского технологического института (Caltech) Сридипа Пала показала универсальные свойства структур квантовой запутанности в высших измерениях, применив методы теоретической физики частиц к квантовой информатике.

Команда сосредоточилась на термической эффективной теории, которая недавно привела к значительным прорывам в анализе многомерных теорий в физике частиц. Этот подход позволяет выявлять универсальные закономерности в сложных системах, используя лишь небольшое количество параметров.

Применив эту теорию к квантовой информатике, исследователи проанализировали поведение энтропии Реньи в многомерных квантовых системах.

Энтропия Реньи характеризуется параметром, называемым числом реплик. Учёные показали, что при малых значениях этого параметра поведение энтропии Реньи универсально определяется всего несколькими величинами, такими как энергия Казимира.

Кроме того, команда выяснила поведение спектра запутанности в области больших собственных значений и исследовала, как меняются универсальные закономерности в зависимости от метода вычисления энтропии Реньи.

Эти результаты справедливы не только для (1+1)-мерных систем, но и для пространств любой размерности, что является важным шагом в понимании квантовой запутанности в высших измерениях.

Следующим шагом станет дальнейшее обобщение и уточнение этого подхода. Работа впервые демонстрирует, что термическая эффективная теория может успешно применяться для изучения структур квантовой запутанности в многомерных системах, и открывает новые возможности для развития этого направления.

Улучшение термической эффективной теории с учётом квантовой информации может углубить понимание структур запутанности в многомерных системах.

С практической точки зрения, полученные результаты могут привести к улучшению методов численного моделирования многомерных квантовых систем, предложить новые принципы классификации квантовых состояний и внести вклад в квантово-информационное понимание гравитации. Эти достижения открывают широкие перспективы для будущих приложений.

Больше информации: Yuya Kusuki et al, Universality of Rényi Entropy in Conformal Field Theory, Physical Review Letters (2025). DOI: 10.1103/fsg7-bs7q

Источник: The Kavli Foundation